| Autore |
Discussione |
|
|
Mr.Dépistage
Nuovo Arrivato
Città: Montpellier
27 Messaggi |
 Inserito il - 15 giugno 2009 : 14:59:08
|
Salve ragazzi sono nuovo... ma ho tanta esperienza in genetica alle spalle, quindi vi posso aiutare... ma in qst momento io ho bisogno di voi... purtroppo ciò ke il mio cervello rifiuta è la probabilità :( allora:
ho questi dati: 1. malattia: emocromatosi genetica (AR)
2. q^2= 1/1600
il problema dice ke ho un paziente di 57 anni affetto da qst malattia quindi aa, lui si sposa, ha 2 figli e uno dei quali si sposa con una certa donna. Qual è la probabilità che il nuovo nato di qst ultima coppia sia malato?
La mia risoluzione è qst: la probabilità del figlio (o dei figli) del paziente malato di essere portatore sano è 1/2 xkè dato ke la malattia è molto frequente (1/1600) ho supposto ke la moglie del paziente malato sia portatrice dell'allele malato (Aa) quindi aa x Aa= 1/2 malato e 1/2 portatore. Poi ho calcolato la frequenza della moglie di qst'ultimo di essere portatrice come 2q (xkè quando q è molto più piccolo di p allora 2pq = 2q)e mi è uscito 1/20. Quindi la probabilità ke qst feto della coppia in causa sia malato è: 1/20 x 1/2 x 1/4 = 1/160
è giusto o occorre utilizzare il teorema di bayes? se si come? GRAZIE (se possib. mi serve al + presto... ho esame di genetica medica a giorni) :(
|
|
|
|
|
GFPina
Moderatore
Città: Milano
8408 Messaggi |
Inserito il - 15 giugno 2009 : 16:07:12
|
Ciao Mr.Dépistage,
benvenuto! 
Citazione:
Messaggio inserito da Mr.Dépistage
la probabilità del figlio (o dei figli) del paziente malato di essere portatore sano è 1/2 xkè dato ke la malattia è molto frequente (1/1600) ho supposto ke la moglie del paziente malato sia portatrice dell'allele malato (Aa) quindi aa x Aa= 1/2 malato e 1/2 portatore.
L'esercizio non ti dice che i figli sono affetti quindi hanno fenotipo sano e l'unica opzione è che siano portatori, visto che dal padre prendono per forza la "a". Non ti interessa sapere com'era la madre.
Citazione:
Messaggio inserito da Mr.Dépistage
Poi ho calcolato la frequenza della moglie di qst'ultimo di essere portatrice come 2q (xkè quando q è molto più piccolo di p allora 2pq = 2q)e mi è uscito 1/20.
 sinceramente a me verrebbe da calcolarmi comunque come 2pq, ma non cambia molto perché avresti: 39/800 anziché 40/800 (1/20), quindi è giustissimo come hai fatto! 
Citazione:
Messaggio inserito da Mr.Dépistage
Quindi la probabilità ke qst feto della coppia in causa sia malato è: 1/20 x 1/2 x 1/4 = 1/160
togliendo 1/2 per le ragioni dette prima sarebbe:
1/20 x 1/4 = 1/80
Vorrei però farti notare un ulteriore "errore", o meglio un fattore che non hai considerato.
Se tu considerassi che non sai il fenotipo dei figli dell'uomo malato (ammettiamo che devono nascere e ti chiede la P degli eventuali nipoti) comunque sai che i figli erediteranno sicuramente dal padre "a", quindi i genotipi possibili sono Aa e aa (con le rispettive P che non sto a calcolare), ma sia Aa che aa possono dar origine ad un figlio malato sposandosi con una donna Aa
Aa x Aa ha 1/4 di P di dare aa
aa x Aa ha 1/4 di P di dare aa
quindi la P finale sarebbe:
P = P figlio (Aa) x 1/4 + P figlio (aa) x 1/2
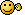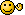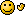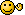
P.S. Dimenticavo, ho scisso il tuo messaggio dalla discussione in cui l'avevi inserito perché è un argomento diverso! |
 |
|
|
Mr.Dépistage
Nuovo Arrivato
Città: Montpellier
27 Messaggi |
Inserito il - 15 giugno 2009 : 17:26:36
|
Ti ringrazio per il benvenuto e per la soluzione...! Cercherò di contribuire anke io su qst forum!
cmq io nn riesco a capire ancora quando si usa il teorema di Bayes, xkè ho appurato ke lo si utilizza nella maggior parte dei problemi in genetica medica, ma in altri ad esempio forse in questo sull'emocromatosi invece no... sapresti dirmi il motivo?
ciao!!! |
|
|
|
GFPina
Moderatore
Città: Milano
8408 Messaggi |
Inserito il - 15 giugno 2009 : 18:34:01
|
Sinceramente non saprei, io non l'ho mai usato!
Ma guardando la definizione su wikipedia: Teorema di Bayes
(premetto che l'esempio che fa io lo risolverei in altro modo e arrivo allo stesso risultato, senza teorema)
se consideriamo:
A = madre Aa
B = feto aa
P(A) = P che la madre sia Aa senza altre informazioni
P(B) = P che il feto sia aa senza altre informazioni
P(B/A) = P che il feto sia aa sapendo che la madre è Aa
ma P(A/B) sarebbe:
P(A/B) = P che che la madre sia Aa sapendo che il feto è aa
che però non è quella che ci interessa calcolare!
e comunque sarebbe:
P(B/A) P(A)
P(A/B) = --------------
P(B)
P(B/A) = 1/4
P(A) = 1/20 (2p come calcolata prima)
P(B) = 1/1600 (che è la frequenza di aa nella popolazione)
1/4 x 1/20
P(A/B) = --------------
1/1600
però rimane il fatto che non è quello che vogliamo trovare!
Non so magari se hai degli esercizi dove sai che si usa il teorema di Bayes prova a postarli!
|
|
|
|
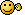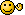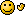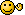Mr.Dépistage
Nuovo Arrivato
Città: Montpellier
27 Messaggi |
Inserito il - 16 giugno 2009 : 11:05:35
|
| mmmmm.... il teorema di Bayes nn è così... cmq provo a postare un altro esercizio x vedere se ho capito bene... |
|
|
|
chick80
Moderatore
Città: Edinburgh
11491 Messaggi |
|
|
Mr.Dépistage
Nuovo Arrivato
Città: Montpellier
27 Messaggi |
Inserito il - 16 giugno 2009 : 13:21:16
|
In genetica medica x calcolare il rischio di ricorrenza di una malattia genetica si utilizza qst teorema ke sarebbe il teorema di Bayes (anke se nn ho + ricordi di matematica classica quindi nn so se qst è il vero o un derivato):
P(C/FN) = [P(FN/C) x P(C)] / [P(FN/C) x P(C) + P(FN/nonC) x P(nonC)]
dove FN=figlio normale et C=conduttrice
ovvero...: la probabilità ke una paziente sia conduttrice è uguale alla probabilità di avere un figlio normale se essa è conduttrice per la prob di esserlo, fratto la prob che il figlio sia normale se essa è conduttrice per la probabilità che sia conduttrice più la probabilità che il figlio sia normale se la madre non è conduttrice per la probab di essere una non conduttrice.
uff complicato da capire... |
|
|
|
GFPina
Moderatore
Città: Milano
8408 Messaggi |
Inserito il - 16 giugno 2009 : 13:52:32
|
per conduttrice immagino tu intenda portatrice... comunque adesso non ho troppo tempo da dedicare alla formula, la rivedo poi con calma.
Rimane il fatto che sia applicando quella formula sia quella che avevo scritto io calcoleresti la probabilità che la madre sia portatrice, non che il feto sia affetto. |
|
|
|
Mr.Dépistage
Nuovo Arrivato
Città: Montpellier
27 Messaggi |
Inserito il - 16 giugno 2009 : 14:02:30
|
ma infatti poi quella probabilità va moltiplicata x 1/4 o x 1/2... dipende dal contesto. Cmq si tranquilla anzi grazie mille! Ah scusa ma traduco dal francese all'italiano quindi conductrice = portatrice :))
Senti ti volevo dire un'altra cosa... emmm... questo tipo di problemi tu li affronti di solito, cioè sei allenata a far ciò o sono reminescenze del passato? Per quanto io condivida il tuo ragionamento vorrei capire se mi "posso fidare" della risoluzione di questi problemi anche perchè ti dico che questo Bayes mi assilla!!! Non ho detto una cattiveria eh :) vorrei solo sapere anche per la mia carriera futura se questi problemi si risolvono realmente così!
Grazie mille, può essere ke posterò altro... tu naturalmente rispondi solo se hai voglia e tempo grazie! ciao |
|
|
|
GFPina
Moderatore
Città: Milano
8408 Messaggi |
Inserito il - 16 giugno 2009 : 14:36:59
|
Si immaginavo fosse una traduzione del Francese tranquillo ci sono abituata, ho un cugino che vive in Francia e sono l'unica che lo capisce quando parla il suo "Italiano"! 
Per la domanda diciamo "NI".
No non li affronto di solito, nel senso che nel mio lavoro non li incontro questi problemi, non ho a che fare con malattie genetiche, però sono sempre qua a rispondere a domande di genetica.
Ma le mie conoscenze derivano da reminiscenze del passato!
In pratica non so come vengano risolti questi problemi, ma immagino si risolvano così... altrimenti perché ci fanno studiare ste cose??? 
comunque con calma cercherò se trovo qualcosa, interessa anche a me sapere questa cosa del Teorema di Bayes (giusto per curiosità) |
|
|
|
Mr.Dépistage
Nuovo Arrivato
Città: Montpellier
27 Messaggi |
Inserito il - 16 giugno 2009 : 14:41:12
|
| Ahia :D questa risposta la temevo... va bene grazie lo stesso!!! Vedo che sei abbastanza in gamba e per ricordare... ricordi!!! Se ne sai di più su quel teorema fammi sapere grazie ;)) |
|
|
|
GFPina
Moderatore
Città: Milano
8408 Messaggi |
Inserito il - 16 giugno 2009 : 17:04:56
|
Ehhhh mi spiace per la risposta, ma così è purtroppo... non ho trovato un posto in campo più genetico!
Comunque riguardo al teorema di Bayes ho trovato questo sito molto interessante: http://www.bayes.it/
anche se non risponde alla nostra domanda!
Però ripensandoci un po'...
con la formula:
Citazione:
P(C/FN) = [P(FN/C) x P(C)] / [P(FN/C) x P(C) + P(FN/nonC) x P(nonC)]
dove FN=figlio normale et C=conduttrice
trovi la P condizionata che la madre sia portatrice sapendo che ha avuto un figlio sano P(C/FN). Ma nel tuo caso non c'è scritto che ha avuto un figlio sano quindi usi la P che sia portatrice a priori (2pq).
Se sapessi che ha avuto un figlio sano e ti chiedesse la P che abbia un secondo figlio affetto allora useresti quella per calcolare la P che sia portatrice.
Con i dati che abbiamo e se non ho fatto errori di calcolo la P a priori è 1/20 come dicevamo (=0,05), se sapessi che ha avuto un figlio sano utilizzeresti Bayes e otterresti 3/79 (=0,038) che è più bassa.
Poi questa P scende man mano che la donna ha figli sani, cioè più figli sani ha minore è la P che sia portatrice e la P tende a zero (ovviamente "teoricamente" perché la donna non avrà mai 100 figli), ma il senso è quello!
Credo che comunque le P che calcoliamo in genere (nel modo che ho fatto io) siano una semplificazione per gli "esercizi di genetica", l'unica cosa di cui sono convinta (diciamo 99% ) è che Bayes in questo caso lo potresti usare solo se sapessi che la donna ha avuto un figlio sano.
Grazie per il complimento comunque:
Citazione:
Messaggio inserito da Mr.Dépistage
Vedo che sei abbastanza in gamba e per ricordare... ricordi!!!
... spero di ricordare giusto! 
 |
|
|
|
Mr.Dépistage
Nuovo Arrivato
Città: Montpellier
27 Messaggi |
Inserito il - 16 giugno 2009 : 17:27:06
|
| ok grazie!!! ora ci penso e ci ripenso e poi rispondo e magari inserisco qlke altro esercizio. |
|
|
|
GFPina
Moderatore
Città: Milano
8408 Messaggi |
Inserito il - 16 giugno 2009 : 23:06:37
|
Allora ho trovato questo "interessante" "pdf" fatto da lucidi scritti a mano! 
(vale la pena guardarlo!): http://medgen.univr.it/didattica/genetica08/turco/Lezi57e58Bayes2008-09.pdf
comunque a parte la difficoltà a decifrarlo avvalora la mia Ipotesi! 
Innanzitutto la formula!
E' giusta quella che abbiamo messo all'inizio io e chick80, ma all'aumentare delle alternative il denominatore diventa una sommatoria:
quindi da qui deriva quello che scrivei tu Mr.Dépistage, avendo 2 alternative.
Detto questo, e ora che mi sono ristudiata il teorema di Bayes! 
In genetica medica il teroema di Bayes lo usi nei seguenti casi:
(e qua copio bellamente dal suddetto file)
1. Eredità Autosomica Dominante: nei casi di
- ridotta penetranza
- esordio tradivo
2. Eredità Diaginica
3. Eredità Autosomica Recessiva
siccome per l'Eredità Autosomica Recessiva mette un esempio in cui considera anche i test diagnostici predittivi, metto quest'esempio anche se sarebbe un caso di X-linked, ma è simile a quello che dicevamo:
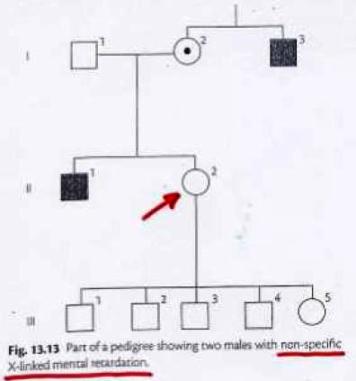
La donna indicata con la freccia ha avuto quattro figli maschi sani e si chiede la P che la 5° figlia femmina sia portatrice.
La P a priori che sia portatrice P(C) è 1/2 e che non sia portatrice P(nonC) è sempre 1/2
la P condizionata di avere un figlio sano se è portatrice è P(FN/C)= 1/2
la P condizionata di avere un figlio sano se non è portatrice è P(FN/nonC)= 1
siccome ha avuto 4 figli sani P(B|A)= (1/2)^4 = 1/16
P(FN/nonC)= 1^4 = 1
quindi mettendo tutto nella formula:
P(C/FN) = [P(FN/C) x P(C)] / [P(FN/C) x P(C) + P(FN/nonC) x P(nonC)]
P(C/FN) = [1/16 x 1/2] / [1/16 x 1/2 + 1 x 1/2] = 1/17
quindi la P che la 5° figlia femmina sia portatrice 1/2 x 1/17 = 1/34
Beh spero che almeno questo ti sia di aiuto!
|
|
|
|
Mr.Dépistage
Nuovo Arrivato
Città: Montpellier
27 Messaggi |
Inserito il - 17 giugno 2009 : 13:02:35
|
| si mi è stato molto di aiuto!!! Grazie... ma prima di darti una risposta sicura mi vado a studiare quelle dispense linkate sopra... nn avevo preso in considerazione il fatto di elevare 1/2 alla 4 figli sani.... mai...! Ti farò sapere. Merci |
|
|
| |
Discussione |
|
Probabilità emocromatosi
