| Autore |
Discussione |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 27 gennaio 2011 : 13:02:55 Inserito il - 27 gennaio 2011 : 13:02:55




|
|
Visto che la forma di un'istogramma varia al variare dei limiti e del numero dei bin, sapete se esiste un criterio per scegliere i parametri necessari a definire un istogramma? Mi sto riferendo ad istrogrammi 3d.
|
|
|
|
|
dallolio_gm
Moderatore
  

Prov.: Bo!
Città: Barcelona/Bologna

2445 Messaggi |
 Inserito il - 27 gennaio 2011 : 13:23:07 Inserito il - 27 gennaio 2011 : 13:23:07





|
Vuoi dire il numero di bins per calcolare l'istogramma?
Dipende da cosa vuoi far vedere e da come utilizzerai il grafico. Per esempio, per una presentazione io non userei un numero di bins alto: giá il fatto che sia un istogramma 3d lo rende complicato, dei contorni troppo frastagliati lo renderebbero difficile da leggere.
Una buona regol è di provare ad aumentare il numero di bins e fermarsi quando non escono picchi nuovi, o quando il profilo generale del grafico non cambia. |
Il mio blog di bioinformatics (inglese): BioinfoBlog
Sono un po' lento a rispondere, posso tardare anche qualche giorno... ma abbiate fede! :-) |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 27 gennaio 2011 : 13:43:51 Inserito il - 27 gennaio 2011 : 13:43:51




|
Esistono varie regole per determinare il numero ottimale di classi, le più usate sono la regola di Sturges (generalmente usata quando si hanno pochi valori, es. meno di 150-200) e quella di Freedman-Diaconis che è generalmente la regola da preferire.
FD definisce la larghezza di ciascun bin come:
2 * IQR * n^(-1/3)
Dove IQR è il range interquartile (= 3° quartile - 1° quartile) e n è il numero di osservazioni
La regola di Sturges invece dice che il numero di bins deve essere
ceil(1+log2(n))
dove n è il numero di osservazioni e ceil è la funzione ceiling (parte intera superiore). |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 27 gennaio 2011 : 22:48:48 Inserito il - 27 gennaio 2011 : 22:48:48




|
| Interessante, non sapevo che esistessero delle regole. In quali circostanze è preferibile usare una regola piuttosto che l'altra? |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 28 gennaio 2011 : 00:00:42 Inserito il - 28 gennaio 2011 : 00:00:42




|
Sono comunque da considerarsi "rules of thumb", cioè non è detto che il numero che ti restituiscono sia quello "corretto", semplicemente funzionano bene nel caso medio.
Il numero di bins "corretto" dipende poi ovviamente anche da quello che stai cercando di mostrare.
Citazione:
In quali circostanze è preferibile usare una regola piuttosto che l'altra?
In generale credo che Sturges possa dare risultati sub-ottimali in determinate circostanze (es. con molte osservazioni), l'altra regola è da preferirsi. |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 28 gennaio 2011 : 11:45:29 Inserito il - 28 gennaio 2011 : 11:45:29




|
Citazione:
Messaggio inserito da chick80
Sono comunque da considerarsi "rules of thumb", cioè non è detto che il numero che ti restituiscono sia quello "corretto", semplicemente funzionano bene nel caso medio.
Il numero di bins "corretto" dipende poi ovviamente anche da quello che stai cercando di mostrare.
Citazione:
In quali circostanze è preferibile usare una regola piuttosto che l'altra?
In generale credo che Sturges possa dare risultati sub-ottimali in determinate circostanze (es. con molte osservazioni), l'altra regola è da preferirsi.
Grazie mille chick, in realtà quello che devo fare io è un po' particolare, in quanto devo convertire un andamento temporale in una matrice attraverso l'algoritmo di rainflow che difficilmente avrai incontrato visto che è usato in ambito ingegneristico e così cercavo qualche regola, visto che non ne ho trovata una. D'altro canto io non ho un numero di osservazioni, visto che queste dipendono dal numero di bin, pertanto credo che non posso usare quelle regole nel mio caso. Ho provato a cercare in rete, ma non ho trovato nulla |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 28 gennaio 2011 : 23:46:25 Inserito il - 28 gennaio 2011 : 23:46:25




|
Citazione:
D'altro canto io non ho un numero di osservazioni, visto che queste dipendono dal numero di bin, pertanto credo che non posso usare quelle regole nel mio caso.
Non capisco questa frase. Se hai dei dati di cui vuoi fare un istogramma avrai per forza un numero di osservazioni... (altrimenti con che dati costruisci l'istogramma?) |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 29 gennaio 2011 : 10:37:01 Inserito il - 29 gennaio 2011 : 10:37:01




|
Citazione:
Messaggio inserito da chick80
Citazione:
D'altro canto io non ho un numero di osservazioni, visto che queste dipendono dal numero di bin, pertanto credo che non posso usare quelle regole nel mio caso.
Non capisco questa frase. Se hai dei dati di cui vuoi fare un istogramma avrai per forza un numero di osservazioni... (altrimenti con che dati costruisci l'istogramma?)
con l'algoritmo di rainflow, il quale converte un andamento temporale in un istogramma, contentente il numero di occorrenze delle ampiezze dei cicli all'interno della time history. In questo link è sicuramente spiegato meglio
http://en.wikipedia.org/wiki/Rainflow-counting_algorithm |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 29 gennaio 2011 : 13:26:38 Inserito il - 29 gennaio 2011 : 13:26:38




|
Citazione:
Messaggio inserito da chick80
Sì, ma la tua time series avrà bene una sampling rate no? Sampling rate * durata = numero di samples.
certamente, però io fisso il numero di bin ed il limite dell'istogramma, e lui discretizza ulteriormente la mia time history in funzione dei due parametri scelti. Con l'ulteriore processo di discretizzazione vengono decise le classi e non dal sampling rate. Spero di essermi spiegato meglio |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 29 gennaio 2011 : 13:40:30 Inserito il - 29 gennaio 2011 : 13:40:30




|
La regola di FD ti permette di scegliere la larghezza dei bins in funzione di sampling rate e IQR.
Ad es. se il tuo segnale in entrata fosse y=sin(5*t), acquisito per 2s a 1KHz, avrai 2000 punti ed un IQR di 1.204720
La regola ti dice quindi che la larghezza ottimale dei bins sarà
2 * IQR * n^(-1/3) = 2 * 1.204720 * 2000^(-1/3) = 0.1912 s
Quindi avrai 2/0.1912 ~= 10 bins |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 29 gennaio 2011 : 14:04:37 Inserito il - 29 gennaio 2011 : 14:04:37




|
Citazione:
Messaggio inserito da chick80
La regola di FD ti permette di scegliere la larghezza dei bins in funzione di sampling rate e IQR.
Ad es. se il tuo segnale in entrata fosse y=sin(5*t), acquisito per 2s a 1KHz, avrai 2000 punti ed un IQR di 1.204720
La regola ti dice quindi che la larghezza ottimale dei bins sarà
2 * IQR * n^(-1/3) = 2 * 1.204720 * 2000^(-1/3) = 0.1912 s
Quindi avrai 2/0.1912 ~= 10 bins
Il metodo di rainflow funziona in maniera diversa. Prova a vedere questo link: http://books.google.com/books?id=mrPFTVr2hH4C&pg=PA79&dq=level+crossing+fatigue&hl=it&ei=qQ9ETe6zNIaSswbYndDCDg&sa=X&oi=book_result&ct=result&resnum=2&ved=0CC0Q6AEwAQ#v=onepage&q=level%20crossing%20fatigue&f=false pag 80 fig 3.2. Supponi che quello sia un segnale che può essere campionato a 20kHz o anche 50KHz, non importa. Poi tu decidi il numero di bin ed il limite dell'istogramma ed il canale viene discretizzato ulteriormente, come nell'immagine in figura che è discretizzato in modo tale che i passi sono: 1 2 3 4 5, e così via. Spero di aver spiegato meglio qual'è il mio dubbio. Intanto grazie per la disponibilità |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 29 gennaio 2011 : 17:09:10 Inserito il - 29 gennaio 2011 : 17:09:10




|
Allora forse non ho capito la domanda...
Tu hai un segnale in entrata, vuoi farne un'istogramma e vuoi sapere il numero di bins, giusto? E' un segnale discreto o continuo (ovvero, deriva da una misurazione o è una funzione matematica)? |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 30 gennaio 2011 : 00:33:14 Inserito il - 30 gennaio 2011 : 00:33:14




|
Citazione:
Messaggio inserito da chick80
Allora forse non ho capito la domanda...
Tu hai un segnale in entrata, vuoi farne un'istogramma e vuoi sapere il numero di bins, giusto? E' un segnale discreto o continuo (ovvero, deriva da una misurazione o è una funzione matematica)?
deriva da misure che ho fatto, ma in realtà se il segnale fosse continuo non cambierebbe nulla. Cmq il numero di campioni del segnale non è correlato al numero di bin dell'istogramma in questione, visto che il numero dei campioni viene definito dopo che ho scelto il numero di bin dell'istogramma ed i suoi limiti. E' un discorso completamente diverso dagli usuali istogrammi che magari si possono incontrare in ambito biologico |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 30 gennaio 2011 : 01:51:48 Inserito il - 30 gennaio 2011 : 01:51:48




|
Scusami ma continuo a non capire... Per fare un'istogramma dividi il range del tuo segnale in bins e conti quanti punti del tuo segnale cadono in ogni bin. Quindi hai per forza un numero di osservazioni, altrimenti non potresti contarle. Che i bin siano 10 o 1000 o 10000000 il numero di questi valori non cambierà. Poi il numero di campioni IN USCITA sarà diverso e dipendente dai bins, questo è ovvio, ma il segnale in entrata sempre quello è.
Citazione:
deriva da misure che ho fatto, ma in realtà se il segnale fosse continuo non cambierebbe nulla.
Cambierebbe perchè non non ha senso fare un istogramma di un segnale continuo. In quel caso produrresti invece la pdf del segnale, non il suo istogramma.
Paper che forse può essere utile
http://www.prognostics.umd.edu/calcepapers/06_NVichare_BinningDensityEstimationLoadParameters_InternationalJrnalPerformabilityEngineering.pdf
|
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 30 gennaio 2011 : 12:52:22 Inserito il - 30 gennaio 2011 : 12:52:22




|
Citazione:
Messaggio inserito da chick80
Scusami ma continuo a non capire... Per fare un'istogramma dividi il range del tuo segnale in bins e conti quanti punti del tuo segnale cadono in ogni bin. Quindi hai per forza un numero di osservazioni, altrimenti non potresti contarle. Che i bin siano 10 o 1000 o 10000000 il numero di questi valori non cambierà. Poi il numero di campioni IN USCITA sarà diverso e dipendente dai bins, questo è ovvio, ma il segnale in entrata sempre quello è.
Citazione:
deriva da misure che ho fatto, ma in realtà se il segnale fosse continuo non cambierebbe nulla.
Ho fatto un po' di confusione. Hai ragione...Scusami
Citazione:
Cambierebbe perchè non non ha senso fare un istogramma di un segnale continuo. In quel caso produrresti invece la pdf del segnale, non il suo istogramma.
Paper che forse può essere utile
http://www.prognostics.umd.edu/calcepapers/06_NVichare_BinningDensityEstimationLoadParameters_InternationalJrnalPerformabilityEngineering.pdf
Mitico...sembra proprio quello di cui avevo bisogno. Coma hai fatto a trovare un paper del genere, io mi ci sono svenato. Adesso me lo leggo per bene, grazie mille. |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 30 gennaio 2011 : 12:58:40 Inserito il - 30 gennaio 2011 : 12:58:40




|
Citazione:
Coma hai fatto a trovare un paper del genere, io mi ci sono svenato. Adesso me lo leggo per bene, grazie mille.
Ho cercato su Google "rainflow Freedman Diaconis"!  |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 30 gennaio 2011 : 17:45:19 Inserito il - 30 gennaio 2011 : 17:45:19




|
avevo provato a cercare rainflow e sturges ma non avevo trovato nulla. Comunque grazie al tuo paper, ho migliorato le ricerche e son riuscito a trovare qualche informazione in più. In soldoni sto usando un software che a partire dagli istogrammi di rainflow lui definisce la distribuzione di probabilità usando un metodo non parametrico, nello specifico Epanechnikov kernel.Sfogliando su diversi paper, ho trovato qualcosa di interessante, tra cui questo, ma non capisco se si riferisce alla dimensione dei bin, visto che parla di kernel bandwidth.
http://urrg.eng.usm.my/index.php?option=com_content&view=article&id=79:introduction-to-probability-density-estimation&catid=31:articles&Itemid=70
In soldoni in quel paper, così come in altri si parla di bin width e poi si passa alla kerner bandwidth. Sono i due in qualche modo correlati?
Non sò se sei competente in questo oppure no, ma magari riesci a darmi altre indicazioni.
Intanto grazie di cuore..mi dai sempre degli ottimi consigli |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 30 gennaio 2011 : 18:41:28 Inserito il - 30 gennaio 2011 : 18:41:28




|
Sì in pratica l'idea è che avendo una serie di dati puoi utilizzare determinate funzioni per stimare la pdf (probability density function).
Esistono vari metodi, che in generale utilizzano una funzione "kernel" (=nocciolo) per stimare la densità di probabilità ad ogni punto a partire da una distribuzione discreta.
In generale una funzione kernel è una funzione reale, non negativa e integrabile.
Deve soddisfare due condizioni:
essere simmetrica rispetto all'asse y, quindi f(x) = f(-x)
il suo integrale da -inf a +inf deve essere = 1
Il kernel di Epanechnicov è una funzione fatta così:

Non so che metodo utilizzi il tuo software, quindi non so dirti più di così.
Se la cosa può essere utile, ti cito la spiegazione del metodo usato dalla funzione density di R:
Citazione:
The algorithm used in ‘density.default’ disperses the mass of the empirical distribution function over a regular grid of at least 512 points and then uses the fast Fourier transform to convolve this approximation with a discretized version of the kernel and then uses linear approximation to evaluate the density at the specified points.
Ci sono anche queste referenze che potrebbero essere utili (se riesci a trovarle!):
Scott, D. W. (1992) Multivariate Density Estimation. Theory, Practice and Visualization. New York: Wiley.
Sheather, S. J. and Jones M. C. (1991) A reliable data-based bandwidth selection method for kernel density estimation. J.
Roy. Statist. Soc. *B*, 683-690.
Silverman, B. W. (1986) Density Estimation. London: Chapman and Hall.
PS: sicuramente nel link che hai indicato quando parla di kernel bandwidth sta parlando dei metodi di stima della pdf, non dei bins dell'istogramma. |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 30 gennaio 2011 : 22:23:25 Inserito il - 30 gennaio 2011 : 22:23:25




|
Citazione:
Messaggio inserito da chick80
Sì in pratica l'idea è che avendo una serie di dati puoi utilizzare determinate funzioni per stimare la pdf (probability density function).
Esistono vari metodi, che in generale utilizzano una funzione "kernel" (=nocciolo) per stimare la densità di probabilità ad ogni punto a partire da una distribuzione discreta.
In generale una funzione kernel è una funzione reale, non negativa e integrabile.
Deve soddisfare due condizioni:
essere simmetrica rispetto all'asse y, quindi f(x) = f(-x)
il suo integrale da -inf a +inf deve essere = 1
Il kernel di Epanechnicov è una funzione fatta così:

Non so che metodo utilizzi il tuo software, quindi non so dirti più di così.
Se la cosa può essere utile, ti cito la spiegazione del metodo usato dalla funzione density di R:
Citazione:
The algorithm used in ‘density.default’ disperses the mass of the empirical distribution function over a regular grid of at least 512 points and then uses the fast Fourier transform to convolve this approximation with a discretized version of the kernel and then uses linear approximation to evaluate the density at the specified points.
Ci sono anche queste referenze che potrebbero essere utili (se riesci a trovarle!):
Scott, D. W. (1992) Multivariate Density Estimation. Theory, Practice and Visualization. New York: Wiley.
Sheather, S. J. and Jones M. C. (1991) A reliable data-based bandwidth selection method for kernel density estimation. J.
Roy. Statist. Soc. *B*, 683-690.
Silverman, B. W. (1986) Density Estimation. London: Chapman and Hall.
PS: sicuramente nel link che hai indicato quando parla di kernel bandwidth sta parlando dei metodi di stima della pdf, non dei bins dell'istogramma.
Allora se leggi il paragrafo due c'è scritto:
Smoothing Parameter
The parameter bin width h will determine the smoothness of the constructed histogram. Small value h produces under-smooth histogram that display an estimate with more variations and spurious bumps and larger h produces over-smooth histogram which almost flat. This bin width h, is sometimes referred as a smoothing parameter or scaling factor. The optimal value of h can be obtained by minimizing the asymptotic mean integrated squared error (AMISE) by making a tradeoff between the squared bias and variance. The equation for optimal bin width is given by the following formula
poi non capisco perchè se ne parte a parlare di kernel bandwidth, anche in altri paper è la stessa cosa. Che non sia importante?
Se ti può essere utile sò che il sw che sto usando usa i kernel di Epanechnicov con adaptive bandwidth.
Intanto grazie mille per la disponibilità e per avermi fatto trovare altri paper interessanti grazie alle tue dritte ;)
|
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 31 gennaio 2011 : 11:48:48 Inserito il - 31 gennaio 2011 : 11:48:48




|
La frase che citi dice molto semplicemente che se usi dei grossi bin perdi di risoluzione e se li usi troppo piccoli puoi creare artificialmente dei picchi che non esistono.
Forse quello che non ti è del tutto chiaro è la differenza fra istogramma e pdf.
In pratica puoi considerare l'istogramma come una "versione discreta" della pdf.
Facciamo un esempio pratico.
Ipotizziamo di misurare l'altezza degli abitanti di un'isola. La popolazione totale è la popolazione dell'isola, diciamo 100000 individui. Ora, noi scegliamo 50 persone e ne misuriamo l'altezza. Otteniamo una serie di valori ad es:
172.4671 181.9730 178.8162 193.3018 181.7546 184.7795 171.2731 190.7180
167.6211 174.6021 181.3483 181.4441 176.9755 191.0976 181.8507 179.5602
174.1672 187.6628 166.2928 214.6545 173.4287 191.4609 183.9294 191.6011
167.7843 173.4232 169.1967 183.4642 162.6341 183.7061 178.6333 206.3606
177.9311 178.3321 169.6498 176.6731 182.7436 186.2598 195.9810 194.5530
178.4756 201.0481 153.3484 189.3430 172.1657 199.8335 174.5484 199.7860
180.6567 151.8202
Possiamo costruire un istogramma di queste misure, ovvero, decidiamo dei bins in cui dividere queste misure e contiamo quanti elementi ci sono in ciascuno di questi bins. Possiamo usare la regola di Fred-Diacones per determinare il numero di bins.
w = 2 * IQR * n^(-1/3) = 2 * 15.31 * 50^(-1/3) = 8.3
Contando che le nostre misure sono fra 151.8 e 214.7 possiamo fare dei bins da 150 a 220 larghi 10 (ribadisco, FD è una "rule of thumb", non è necessario usare esattamente 8.3, il valore si decide un po' a occhio).
Otteniamo un istogramma così fatto:
Immagine:
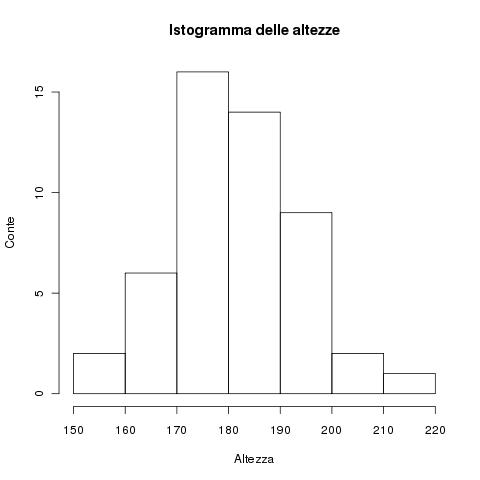
15,12 KB
E la pdf e i kernel cosa ci azzeccano qui dentro? L'istogramma mi dà un'indicazione della distribuzione della popolazione a partire da un campione della stessa. Non è però stato generato da TUTTA la popolazione (cioè dalle altezze di tutti i 100000 individui).
Siccome non possiamo misurare tutti gli abitanti dell'isola decidiamo allora di estrapolare la distribuzione di tutta la popolazione, creando una probability density function (pdf). Ovvero creiamo una curva che associa ad ogni possibile valore di altezza x una certa probabilità. Mi dice ad es. che probabilità ho di avere una persona di quella popolazione con altezza 158.3? E questo per ogni singolo valore di altezza possibile.
Per estimare questa curva si utilizzano delle funzioni kernel (la spiegazione matematica è nei papers che ti ho linkato prima) e questo ci permette di estrapolare la curva continua a partire dalla nostra distribuzione discreta. Nota che si usano i dati grezzi NON le conte dell'istogramma per fare questo tipo di analisi. Infatti la generazione della pdf non richiede di generare prima un istogramma.
La scelta del kernel può influenzare un po' la forma della pdf generata. Ad es. con i nostri dati possiamo generare questa pdf (in nero ho usato un kernel gaussiano, in rosso un kernel di Epanechnikov). Ho sovrapposto le curve all'istogramma.
Immagine:
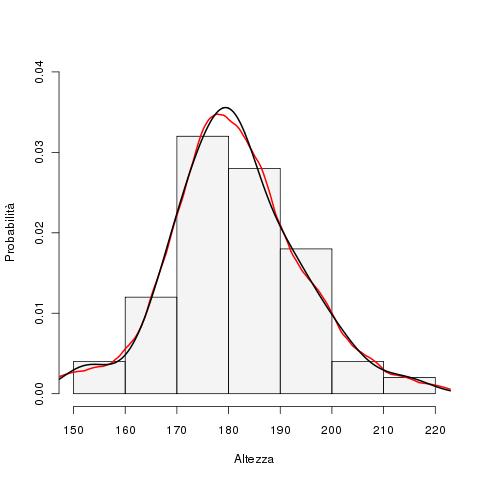
17,98 KB
L'interpretazione è un pochino diversa quando si parla di time series, ma l'idea alla base è la stessa. |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 31 gennaio 2011 : 15:43:46 Inserito il - 31 gennaio 2011 : 15:43:46




|
| quindi in soldoni per avere la pdf non è necessario calcolare un istogramma, giusto? A questo punto quello che non mi è chiaro è come viene calcolata la pdf dalle time history, senza calcolare l'istogramma |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 31 gennaio 2011 : 17:09:30 Inserito il - 31 gennaio 2011 : 17:09:30




|
La stima della pdf non è proprio semplicissima (matematicamente parlando).
Il metodo di cui hai visto parlare nei vari papers è chiamato kernel density estimation o metodo della finestra di Parzen-Rosenblatt.
Questi sono i papers originali dei due matematici che hanno sviluppato questa metodica (nota che sono articoli molto matematici, che richiedono conoscenze matematiche/statistiche piuttosto buone anche solo per comprendere che diavolo c'è scritto!):
Remarks on Some Nonparametric Estimates of a Density Function - Rosenblatt 1956
On Estimation of a Probability Density Function and mode - Parzen 1962
In pratica credo che questa immagine faccia capire bene il procedimento teorico: per ogni elemento misurato costruisci una gaussiana (o la funzione kernel che stai usando). La somma di queste funzioni ti dà la kernel density estimation. In pratica vengono utilizzati altri algoritmi più complessi ma molto più veloci.
Nell'immagine hai a sinistra l'istogramma (per confronto) e a destra la kernel estimation: le linee nere sono i vari punti misurati, in rosso i vari kernel che sono sommati a dare la stima della pdf (in blu).

Wikipedia ha una spiegazione più estesa: http://en.wikipedia.org/wiki/Kernel_density_estimation |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 31 gennaio 2011 : 21:32:59 Inserito il - 31 gennaio 2011 : 21:32:59




|
Citazione:
Messaggio inserito da chick80
La stima della pdf non è proprio semplicissima (matematicamente parlando).
Il metodo di cui hai visto parlare nei vari papers è chiamato kernel density estimation o metodo della finestra di Parzen-Rosenblatt.
Questi sono i papers originali dei due matematici che hanno sviluppato questa metodica (nota che sono articoli molto matematici, che richiedono conoscenze matematiche/statistiche piuttosto buone anche solo per comprendere che diavolo c'è scritto!):
Remarks on Some Nonparametric Estimates of a Density Function - Rosenblatt 1956
On Estimation of a Probability Density Function and mode - Parzen 1962
In pratica credo che questa immagine faccia capire bene il procedimento teorico: per ogni elemento misurato costruisci una gaussiana (o la funzione kernel che stai usando). La somma di queste funzioni ti dà la kernel density estimation. In pratica vengono utilizzati altri algoritmi più complessi ma molto più veloci.
Nell'immagine hai a sinistra l'istogramma (per confronto) e a destra la kernel estimation: le linee nere sono i vari punti misurati, in rosso i vari kernel che sono sommati a dare la stima della pdf (in blu).

Wikipedia ha una spiegazione più estesa: http://en.wikipedia.org/wiki/Kernel_density_estimation
mmm non ho ste grandi conoscenze matematiche per riuscire a capire queste cose, anche se un po' ci ho provato perchè ho trovato una tesi di dottorato su questo argomento. Ho capito la filosofia, anche se poi non capisco come viene applicata la cosa. In verità non ho interesse a sapere come funziona il sw per poter replicare o fare modifiche sul metodo, vorrei saperne di più perchè con questo software sto ottenendo dei valori poco credibili se confrontati con la biografia, e quindi vorrei capire se è un mio errore o altro. La cosa strana, è che nel fare questa operazione il sw non ha delle impostazioni, ma prende esclusivamente in input gli istogrammi |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 07 febbraio 2011 : 23:12:51 Inserito il - 07 febbraio 2011 : 23:12:51




|
| allora ho pistolato un po' con la cosa...finalmente ho ottenuto dei risultati credibili, è bastato esclusivamente moltiplicare le frequenze degli istogrammi per un fattore 10 e finalmente ottengo una forma dell'istogramma che ricalca quello dei valori misurati.Giustamente guardando la teoria, non riesco a capire come questa cosa possa influenzare la stima della distribuzione di probabilità, visto che la banda del kernel dipende dal numbero di bin e dalla dispersione dei dati. C'è qualcosa che mi sfugge? |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 08 febbraio 2011 : 06:19:38 Inserito il - 08 febbraio 2011 : 06:19:38




|
Strano, se moltiplichi tutto per 10 la forma dovrebbe restare la stessa.
A questo punto bisognerebbe vedere esattamente che algoritmo è usato dal tuo software... |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
Discussione |
|








