Quanto è utile/interessante questa discussione:
| Autore |
Discussione |
|
|
serbring
Utente Junior
486 Messaggi |
 Inserito il - 31 marzo 2011 : 13:24:49
|
Ho un problema di statistica che non sò bene come risolvere. Ho un macchinario che può essere usato in 4 modalità di lavoro: A, B, C e D. Ho formulato dei questionari a circa 50 persone in cui ho chiesto nell'arco di un anno quante ore all'anno lo utilizzano (nh) e come, ottenendo quindi le percentuali delle ore di utilizzo in ciascuna modalità (A%, B%, C% e D%; A%+B%+C%+D%=100). A sua volta per ciascuna operazione facendo delle misure ricavo un numero che indica quanto ciascuna lavorazione è pericolosa in un ora di utilizzo (questi numeri li chiamo da per l'ultizzo a, db per l'utilizzo b, dc per l'utilizzo c e dd per l'utilizzo d). A sua volta la pericolosità globale nell'utilizzo annuale (che chiamo con D) vale:
D=nh*(da*A%+db*B%+dc*C%+dd*D%)=nh*(da*A%+db*B%+dc*C%+dd*(1- A%-B%-C%))
I parametri nh, A%, B%, C% e D% sono ricavati dai questionari e pertanto sono delle variabili casuali. Devo trovare qual'è il valore di D tale per cui il 95% della popolazione mi sollecita meno il macchinario in un anno di utilizzo (lo chiamiamo D95). A sua volta dovrò anche trovare qual'è quella combinazione di utilizzi che fà sì di avere D95 (questi valori li chiamo A95%, B95%, C95% e D95%).
Anche nh sarà una variabile casuale, allora stavo pensando di prendere il 95° percentile di nh (P(x<nh)<0.95). A sua volta D sarà una variabile casuale con una sua distribuzione di probabilità in funzione di A%, B%, C% e stavo pensando di analizzare A%, B% e C% come se queste avessero delle distribuzioni di probabilità univariate e quindi D sarà dato dalla somma di diverse distribuzioni di probabilità scalate da grandezze scalari. E' secondo voi questo un metodo corretto di agire? Da questo riuscirò a ricavare D95, ma come fare per ricavare A95%, B95%, C95% e D95%? Spero di aver correttamente illustrato il mio problema, se no cercherò di formularlo meglio.
|
|
|
|
|
serbring
Utente Junior
486 Messaggi |
Inserito il - 11 aprile 2011 : 13:59:17
|
| Nessuno ha qualche idea da consigliarmi? :( |
 |
|
|
chick80
Moderatore
Città: Edinburgh
11491 Messaggi |
Inserito il - 11 aprile 2011 : 14:32:50
|
Hai fatto bene a riuppare il topic, l'avevo letto l'altro giorno e poi mi sono dimenticato di rispondere.
Citazione:
A sua volta dovrò anche trovare qual'è quella combinazione di utilizzi che fà sì di avere D95 (questi valori li chiamo A95%, B95%, C95% e D95%).
Il problema è che, essendo le variabili indipendenti fra loro non avrai semplicemente una combinazione. Ossia, puoi utilizzare tanto la modalità A e pochissimo D o viceversa ed ottenere lo stesso valore totale...
Quello che non capisco è la tua definizione di X95.
Tu dici:
Citazione:
Devo trovare qual'è il valore di D tale per cui il 95% della popolazione mi sollecita meno il macchinario in un anno di utilizzo (lo chiamiamo D95)
Parliamo di sollecitazione o di pericolosità? Come sono collegati i due parametri? Immaginando che siano linearmente dipendenti, cosa vuol dire che il 95% della popolazione sollecita meno il macchinario? Il valore di D che sollecita meno il macchinario è, ovviamente, 0%! Oppure vuoi trovare la distribuzione di D% nella popolazione degli intervistati e trovare il 5° centile di questa distribuzione?
Io vedo questo tipo di problema di fatto come una minimizzazione (altrimenti detta ottimizzazione) in uno spazio a 4 parametri (3, contando che la somma dei 4 è fissa).
Wikipedia ha una pagina piena di links a riguardo.
Se lavori in R puoi usare la funzione optim per risolvere questo tipo di problemi.
La pagina del manuale
Vedo se riesco a scriverti un'esempietto veloce veloce :)
PS: per evitare confusione fra D (totale) e D (metodo D) io cambierei nomenclatura... ad es. puoi chiamare il totale T. |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
|
|
|
serbring
Utente Junior
486 Messaggi |
Inserito il - 12 aprile 2011 : 10:39:30
|
Ti ringrazio per la risposta Chick, credo di essermi spiegato male: supponiamo di avere 3 persone che usano questo macchinario, alla quale ho sottoposto il questionario ottenendo per l'operatore 1; A%=10%, B%=30%, C% 40%, D%=20 ed un utilizzo di 500h/anno; per l'operatore 2; A%=50%, B%=5%; C%=15%; D%=30 ed un utilizzo di 200h/anno; per l'operatore 3: A%=80%, B%=0%, C%=10%, D%=10% ed un utilizzo di 100h/anno. A sua volta ciascun utilizzo è caratterizzato da un suo livello di intensità oraria dell'operazione, è una sorta di danneggiamento della macchina e mi dice quanto questa è stata sfruttata se rapportata alla vita totale del macchinario. Questo valore lo chiamo dA per l'operazione A, dB, per l'operazione B e dC per l'operazione C e dD per l'operazione D. Se il D totale (che ora chiamo T :D) è uguale ad 1 la macchina si romperà. Affinchè il progetto del macchinario sia buono sarebbe il caso che la maggior parte della popolazione, durante l'utilizzo del macchinario non raggiunga tale valore e pertanto dovrò scegliere i parametri della macchina in modo tale che il 95% della popolazione durante l'utilizzo della macchina mi raggiunga un T<1. Non posso considerare il 100% della popolazione per ovvi motivi.
Questa è la formula per ricavare T:
T=nh*(da*A%+db*B%+dc*C%+dd*D%)=nh*(da*A%+db*B%+dc*C%+dd*(1- A%-B%-C%))
T è dipendente dal numero di ore di utilizzo, visto che più uso la macchina e più T è grande ed inoltre sarà anche funzione della combinazione di valori A%, B%, C%, D%. Nonostante l'operatore 3 sia quello che utilizza per meno tempo la macchina, potrebbe anche essere quello che me la danneggia di più la macchina perché l'utilizzo A è molto più impegnativo degli altri. A tale punto mi chiedo:
dai dati dei questionari (nh, A%, B%, C%, D%) come è possibile ricavare quella combinazione di tali valori tale per cui il 95% della popolazione raggiunga un T<1?
Spero di essermi spiegato meglio :) |
|
|
|
chick80
Moderatore
Città: Edinburgh
11491 Messaggi |
|
|
chick80
Moderatore
Città: Edinburgh
11491 Messaggi |
Inserito il - 12 aprile 2011 : 16:18:42
|
Stavo pensando che la tua formula non limita necessariamente T a 1, a meno che il numero massimo di ore non sia limitato...
Ad ogni modo, a parte il valore assoluto di T, che poco ci importa, ho fatto un piccolo test in R.
Per semplicità immaginiamo che le modalità d'uso siano 3 e non 4 (puoi fare lo stesso con 4 ma ovviamente devi aggiungere una dimensione al tutto)
Quindi avrai
T = da * A + db * B + dC * (100 - A - B)
Bisogna già dire che ovviamente fissati A e B, C sarà linearmente dipendente da questi due, ad es:
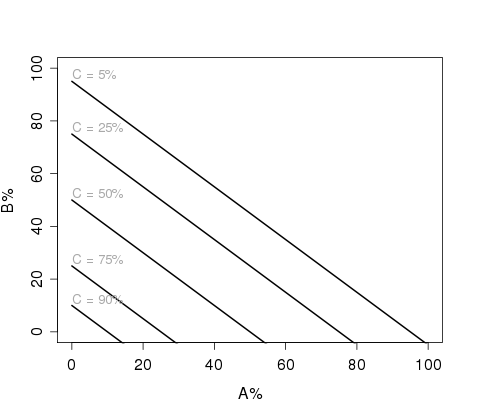
qui vedi rappresentati varie "isolinee" di C% nello spazio A%-B%. Aggiungendo anche D avrai una simile rappresentazione tridimensionale.
Adesso, consideriamo il danno totale:
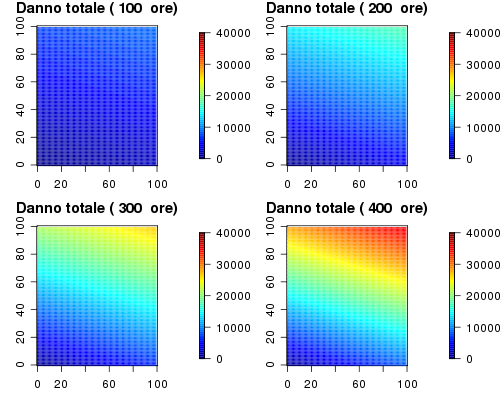
Qui per ogni punto (A%; B%) ho calcolato C% (che come visto sopra è fisso) e poi calcolato il danno totale, in funzione del numero di ore di utilizzo.
Ho usato dA = 0.2, dB = 0.7 e dC = 0.01
Come puoi vedere (e come si capiva già dalla formula) si tratta di un'altra relazione lineare. Essendo C il metodo che comporta meno danno avrai meno danno totale quando C% > A% e B%, ovvero nell'angolo in basso a sinistra (vedi anche il grafico di sopra).
===
Ora, per arrivare alla tua questione del 95%. Come puoi vedere dai grafici di sopra, non c'è una soluzione unica. Puoi avere delle regioni nello spazio dei parametri dove lo sforzo totale è minore di un certo valore, ma ci saranno infinite combinazioni dei 4 parametri possibili.
|
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
|
|
|
serbring
Utente Junior
486 Messaggi |
Inserito il - 13 aprile 2011 : 00:07:40
|
Citazione:
Stavo pensando che la tua formula non limita necessariamente T a 1, a meno che il numero massimo di ore non sia limitato...
Diciamo che T=1 è una soglia teorica oltre al quale il componente si romperebbe. Come tutti sappiamo alla fin fine un macchinario a forza di usarlo si rompe. (Almeno quelli moderni). Quindi alla fine quello che m'importa è che in fase di progetto il macchinario si rompe dopo un certo numero di tempo. Dopo quanto? Dipende dal target che un'azienda si pone: ad esempio se l'azienda vuole che la macchina deve durare almeno 10 anni, verrà progettata in modo tale che il 95% della popolazione in 10 anni di utilizzo non la romperà, o più precisamente che per almeno un certo numero di ore di utilizzo equivalenti a 10 anni di utilizzo. Come trovo questo numero di ore? Dai questionari. Ma quale utilizzo usare? Usando il mio esempio, quello dell'operatore C o dell'operatore A o B? Qui sorgono i problemi.
Citazione:
Ad ogni modo, a parte il valore assoluto di T, che poco ci importa, ho fatto un piccolo test in R.
Per semplicità immaginiamo che le modalità d'uso siano 3 e non 4 (puoi fare lo stesso con 4 ma ovviamente devi aggiungere una dimensione al tutto)
Quindi avrai
T = da * A + db * B + dC * (100 - A - B)
Bisogna già dire che ovviamente fissati A e B, C sarà linearmente dipendente da questi due, ad es:
qui vedi rappresentati varie "isolinee" di C% nello spazio A%-B%. Aggiungendo anche D avrai una simile rappresentazione tridimensionale.
Adesso, consideriamo il danno totale:
Qui per ogni punto (A%; B%) ho calcolato C% (che come visto sopra è fisso) e poi calcolato il danno totale, in funzione del numero di ore di utilizzo.
Ho usato dA = 0.2, dB = 0.7 e dC = 0.01
Come puoi vedere (e come si capiva già dalla formula) si tratta di un'altra relazione lineare. Essendo C il metodo che comporta meno danno avrai meno danno totale quando C% > A% e B%, ovvero nell'angolo in basso a sinistra (vedi anche il grafico di sopra).
===
Ora, per arrivare alla tua questione del 95%. Come puoi vedere dai grafici di sopra, non c'è una soluzione unica. Puoi avere delle regioni nello spazio dei parametri dove lo sforzo totale è minore di un certo valore, ma ci saranno infinite combinazioni dei 4 parametri possibili.
Ho capito la questione, a questo punto mi verrebbe da pensare ad una cosa:…in realtà ho proposto una versione semplificata del mio problema. In un macchinario ho diversi componenti, che si possono rompere: pensa magari ad una macchina, c'è il motore, il telaio e così via, pertanto io non ho un solo T, ma ne ho diversi, uno per ciascun macro componente. Il fatto di avere diversi T e quindi più equazioni mi consente di ridurre il numero di possibili combinazioni dei parametri?
|
|
|
|
chick80
Moderatore
Città: Edinburgh
11491 Messaggi |
Inserito il - 13 aprile 2011 : 12:02:38
|
Hmmmm... mi sa che un'esatta trattazione statistica del problema esula un po' dalle mie conoscenze.
Una cosa che potresti fare è prendere ad es. il 25o e 75o percentile della distribuzione dei 3 metodi meno dannosi.
Costruisci poi un grafico 3D simile a quello che ho costruito di sopra.
In questo modo puoi costruire una regione di utilizzo consigliato del metodo più dannoso.
Ad es. (rifaccio l'esempio solo con 3 variabili) supponiamo questa volta che C sia il metodo più dannoso per la macchina.
Mettiamo dA = 0.2, dB = 0.01 e dC = 0.7
Gli operai di una ditta usano la macchina per 100h/anno e i percentili 25 e 75 di A% sono 30 e 75, di B% sono 20 e 45
Possiamo quindi trovare una regione nel piano A%/B% dove si trova il 50% della popolazione
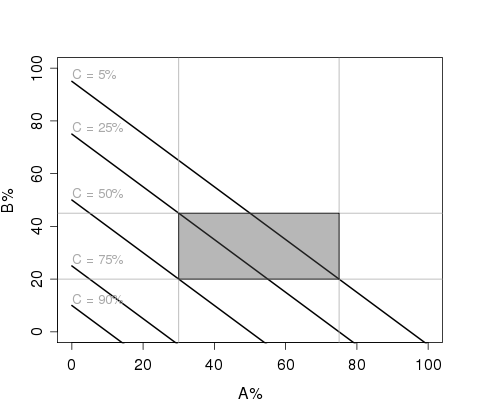
Ora possiamo guardare i valori di stress totale in quella regione del piano e vedere a quale valore max di C% corrisponde il max valore di stress tollerato.
Probabilmente ci sono metodi più appropriati per questo genere di cose, ma dovresti forse guardare un po' su dei libri o dei siti più puntati all'ingegneria... |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
|
|
|
serbring
Utente Junior
486 Messaggi |
Inserito il - 13 aprile 2011 : 17:54:05
|
Citazione:
Messaggio inserito da chick80
Hmmmm... mi sa che un'esatta trattazione statistica del problema esula un po' dalle mie conoscenze.
Una cosa che potresti fare è prendere ad es. il 25o e 75o percentile della distribuzione dei 3 metodi meno dannosi.
Costruisci poi un grafico 3D simile a quello che ho costruito di sopra.
In questo modo puoi costruire una regione di utilizzo consigliato del metodo più dannoso.
Ad es. (rifaccio l'esempio solo con 3 variabili) supponiamo questa volta che C sia il metodo più dannoso per la macchina.
Mettiamo dA = 0.2, dB = 0.01 e dC = 0.7
Gli operai di una ditta usano la macchina per 100h/anno e i percentili 25 e 75 di A% sono 30 e 75, di B% sono 20 e 45
Possiamo quindi trovare una regione nel piano A%/B% dove si trova il 50% della popolazione
Ora possiamo guardare i valori di stress totale in quella regione del piano e vedere a quale valore max di C% corrisponde il max valore di stress tollerato.
Probabilmente ci sono metodi più appropriati per questo genere di cose, ma dovresti forse guardare un po' su dei libri o dei siti più puntati all'ingegneria...
Ti ringrazio Chick. Ho provato a studiare su qualche libro, ma non ho trovato la risposta alla mia domanda. Ho trovato un paio di paper che potrebbero fare al mio caso, ma non riesco a trovarli in alcun modo, ho anche scritto al presunto editore della rivista ed all'autore, entrambi non mi hanno risposto....sinceramente pensavo che fosse un problema molto più semplice. Grazie mille Chick mi hai dato un paio di spunti interessanti...proverò a rifletterci su... |
|
|
|
serbring
Utente Junior
486 Messaggi |
Inserito il - 14 giugno 2011 : 16:03:50
|
| Ho trovato un paper nel quale il mio problema viene approcciato in maniera differente utilizzando un metodo montecarlo. Sto cercando di capirci qualcosa. Comunque mi son reso conto che nel mio metodo non ho tenuto conto di un fatto: visto che in realtà le vere modalità di funzionamento non sono quattro, bensì una ventina, con delle piccole differenze l'una dall'altra, pertanto per pragmatismo ho suddiviso le modalità di funzionamento in sole 4 macro categorie, che sono quelle realmente diverse tra loro. D'altro canto ho testato il macchinario in ogni possibile condizione di lavoro, facendo diverse ripetizioni perchè il processo è in qualche modo casuale. Inoltre ho supposto che per ciascusa macro categoria di funzionamento il macchinario sia sottoposto alla sotto modalità più impegnativa per l'intero tempo. Attualmente ho supposto che la sotto modalità più impegnativa sia quella la cui intensità misurata è la più elevata, ma non è un metodo corretto, perchè potrei essermi trovato a fare la misura in una condizione sfortunata e improbabilmente impegnativa, mentre invece in quella che è solitamente più impegnativa, mi sono ritrovato in una condizione improbabilmente non impegnativa. A questo punto mi chiedo: esiste un metodo statistico per affermare qual'è la condizione più impegnativa? In soldoni il mio problema si traduce in questo modo qua: per ciascuna sotto modalità ho diversi array o serie di numeri del tipo a1=[a11 a12 a13 a14]; a2=[a21 a22 a23 a24]; a3=[a31 a32 a33 a34] e così via; esiste un modo per dire che nel 95% il vettore a1 è più alto? Magari calcolando le distribuzioni di probabilità per ciascun array e prendendo il valore che ha una X(p<0.95) più alto? |
|
|
|
serbring
Utente Junior
486 Messaggi |
Inserito il - 19 giugno 2011 : 19:34:16
|
| nessuno sà darmi un consiglio? |
|
|
| |
Discussione |
|
|
|
Quanto è utile/interessante questa discussione:
| MolecularLab.it |
© 2003-18 MolecularLab.it |
|
|
|
Come approcciare questo problema?
Guide tools online
