Quanto è utile/interessante questa discussione:
| Autore |
Discussione |
|
|
Geeko
Utente
 
Città: Milano

1043 Messaggi |
 Inserito il - 02 novembre 2011 : 19:09:07 Inserito il - 02 novembre 2011 : 19:09:07




|
Carenza matematica assodata ( ) ormai mi imbatto sempre più spesso in grafici costruiti su scala semilogaritmica...ho capito solo che con questo si intende che una delle due variabili (in ascisse o ordinate) è espressa non con suo effettivo valore, ma in scala logaritmica. ) ormai mi imbatto sempre più spesso in grafici costruiti su scala semilogaritmica...ho capito solo che con questo si intende che una delle due variabili (in ascisse o ordinate) è espressa non con suo effettivo valore, ma in scala logaritmica.
Ora, pur sapendo cos'è un logaritmo, in cosa consiste la scala logaritmica?
Cioè esprimo non il mio valore come "x" ma come "log(x)"?
|

|
|
|
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 02 novembre 2011 : 21:07:58 Inserito il - 02 novembre 2011 : 21:07:58




|
Sì e no...
In realtà esprimi sempre il tuo valore come x ma uno o entrambi gli assi non sono lineari. Ossia, mentre in un grafico lineare la distanza fra 1 e 2 è la stessa che fra 5 e 6 o fra 10234 e 10235, su un asse logaritmico la distanza fra 10 e 100 è la stessa che fra 100 e 1000 |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
Giuliano652
Moderatore
   

Prov.: Brescia

6941 Messaggi |
|
|
Geeko
Utente
 

Città: Milano

1043 Messaggi |
 Inserito il - 03 novembre 2011 : 09:13:54 Inserito il - 03 novembre 2011 : 09:13:54




|
Allora, i grafici di Giuliano mi sono chiari. 
Per quello detto da Chick quindi avrei un asse delle ascisse del tipo:

Ma la situazione tra due "unità" com'è? Tipo nell'intervallo [10;100], o [100;1000], i valori si susseguono linearmente? Oppure in che altro modo? Esponenziale?  |

|
 |
|
|
Giuliano652
Moderatore
   

Prov.: Brescia

6941 Messaggi |
|
|
Glubus
Utente Junior



156 Messaggi |
 Inserito il - 03 novembre 2011 : 11:55:07 Inserito il - 03 novembre 2011 : 11:55:07




|
la trasformazione logaritmica dei dati ha tante belle caratteristiche (in particolare per gli statistici).
Anzitutto ti invito a considerare che una rappresentazione grafica (tipicamente in questi casi uno scatterplot) è la rappresentazione di un "modello" di relazione fra due variabili. Tipicamente questo tipo di rappresentazione sottointende la regressioe di una variabile sull'altra.
La trasformazione logaritmica di una variabile corrisponde concettualmente al passaggio da un modello "additivo" ad uno "moltiplicativo".
Ad esempio, se consideriamo la regressione di Y su X, cercando di stabilire E(Y|X=x_i) e cioè il valore atteso di Y dato un certo valore x_i, avremo una variazione attesa di Y di un certo valore (Beta) per ogni aumento di una unità di X (ricordo che nel modello di regressione lineare semplice Y~Alfa + Beta*X + un errore residuo) e ti puoi persuadere di questa relazione sostituendo due valori arbitrari (a e b) alla equazione di regressione:

Se operi la trasformazione logarimica della variabile indipendente avrai invece

che evidenzia come l'incremento nella variabile dipendente (Y) non dipenda più dalla differenza ma dal rapporto dei valori di x_b e x_a.
Cioè la variazione di y per un raddoppio di x sarà lo stesso per un passaggio di x da 1 a 2 cosi come da 10 a 20 o da 1000 a 2000 e sarà in particolare beta*log(2).
Un altro modo di pensare all'effetto della trasformazione logaritmica è questa da meno "peso" ai valori più estremi.
La trasformazione logaritmica è inoltre concettualmente legata alla espessione del valore atteso come media geometrica.
Spero di non avrti fatto più confusione che chiarezza.
Stefano
[quote]Messaggio inserito da Geeko
Carenza matematica assodata ( ) ormai mi imbatto sempre più spesso in grafici costruiti su scala semilogaritmica...ho capito solo che con questo si intende che una delle due variabili (in ascisse o ordinate) è espressa non con suo effettivo valore, ma in scala logaritmica. ) ormai mi imbatto sempre più spesso in grafici costruiti su scala semilogaritmica...ho capito solo che con questo si intende che una delle due variabili (in ascisse o ordinate) è espressa non con suo effettivo valore, ma in scala logaritmica.
Ora, pur sapendo cos'è un logaritmo, in cosa consiste la scala logaritmica?
Cioè esprimo non il mio valore come "x" ma come "log(x)"? ] |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
|
|
Geeko
Utente
 

Città: Milano

1043 Messaggi |
 Inserito il - 03 novembre 2011 : 21:56:57 Inserito il - 03 novembre 2011 : 21:56:57




|
Citazione:
Spero di non avrti fatto più confusione che chiarezza.
Stefano
Premesso che non ho la più pallida idea di cosa sia una regressione seguendo le relazioni che hai messo e il tuo ragionamento penso di aver capito cosa intendi. seguendo le relazioni che hai messo e il tuo ragionamento penso di aver capito cosa intendi.
Quindi quali sono i vantaggi di usare una scala logaritmica per esprimere dei valori o per costruire un grafico?
Se prendo come esempio la classica scala del pH, dove sappiamo che il pH è definito come pH = -log[H+] e mettiamo per semplicità che il range di valori che [H+] può assumere sia da 1M a 10^(-14)M. Quindi se volessi rappresentare la concentrazione [H+] (la penso come la variabile x) avrei un asse con un vastissimo range di valori infinitamente piccoli e difficili da rappresentare, e se immaginariamente mettessi un punto in corrispondenza di un valore, a caso, e poi proseguissi a mettere punti solo in corrispondenza dei valori pari a "dieci volte" il valore del punto precedente, otterrei dei punti distribuiti non linearmente, ma esponenzialmente lungo l'asse (es. 3, 30, 300, 3000...). Quindi sarebbe difficile e poco pratico rappresentarli graficamente (e anche scriverli ogni volta).
Quindi se ora li inserisco in una funzione logaritmica semplifico il tutto dato che passo da considerare la differenza tra due punti consecutivi a considerarne il rapporto, che è costante. I valori che ottengo dopo l'applicazione del logaritmo quindi sono distribuiti linearmente e quindi sono equidistanti tra loro (e più facili da rappresentare).
Tornando all'esempio del pH ottengo valori compresi tra 0 e 14, in cui la variazione di 1 unità di pH corrisponde ad una variazione di 10 volte la concentrazione di H+.
Ora però, nei grafici che incontro non si riporta il valore logaritmico della grandezza considerata...ma invece si "adatta" l'asse, o meglio la distribuzione dei suoi punti in modo da ottenere una certa linearità dei valori che hanno lo stesso rapporto tra loro (intendo che la distanza tra 30 e 300 risulta la stessa che tra 300 e 3000 e così via).
Vi prego, ditemi se è giusto  e dove ho sbagliato! e dove ho sbagliato!
ps. scusate il linguaggio matematico scadente, ma io e la matematica abbiamo un rapporto di amore-odio da sempre XD
E ho un'ultimo mega dubbio da risolvere, ma prima vediamo qui... |

|
 |
|
|
Glubus
Utente Junior



156 Messaggi |
 Inserito il - 04 novembre 2011 : 07:29:41 Inserito il - 04 novembre 2011 : 07:29:41




|
Citazione:
Messaggio inserito da Geeko
...
Ora però, nei grafici che incontro non si riporta il valore logaritmico della grandezza considerata...ma invece si "adatta" l'asse, o meglio la distribuzione dei suoi punti in modo da ottenere una certa linearità dei valori che hanno lo stesso rapporto tra loro (intendo che la distanza tra 30 e 300 risulta la stessa che tra 300 e 3000 e così via).
...
Hai colto il punto.
Non ti far distrarre dalla scala in cui esprimi le "etichette" della variabile trasformata, che potranno essere sia il logaritmo stesso (nel caso del pH) o il valore naturale corrispondente (l'antilogaritmo): la scala sottostante è sempre logaritmica.
|
 |
|
|
Geeko
Utente
 

Città: Milano

1043 Messaggi |
 Inserito il - 05 novembre 2011 : 14:03:45 Inserito il - 05 novembre 2011 : 14:03:45




|
Ora una domanda direttamente collegata alla prima 
Ho due esempi di grafici dose-effetto di un farmaco, dove quindi si esprime l'effetto scatenato (espresso in percentuale) in funzione della dose di farmaco somministrata. Quindi ho la mia dose [D] come variabile indipendente, e l'effetto [E] come quella dipendente.
Ora, i due grafici differiscono solo nel fatto che il primo (1) usa una semplice scala lineare per le dosi di farmaco; il secondo (2) invece usa una scala logaritmica sull'asse [D].
(1)

(2)

La domanda è: perché si passa da una funzione iperbolica (1) ad una sigmoide (2)?  |

|
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 05 novembre 2011 : 14:52:20 Inserito il - 05 novembre 2011 : 14:52:20




|
Citazione:
La domanda è: perché si passa da una funzione iperbolica (1) ad una sigmoide (2)?
Non si passa da un'iperbole (anche se non è proprio un'iperbole, ma chiamiamola così) ad una sigmoide. Il rapporto tra le due variabili è sempre lo stesso, semplicemente cambi il sistema di riferimento in cui disegni il grafico.
Sei passato da uno spazio lineare ad uno spazio semi-logaritmico, quindi ad es. quello che prima era una retta diventerà una curva. Ma è solo un problema "grafico" non hai cambiato la relazione fra x e y.
Per tornare al tuo esempio del pH:
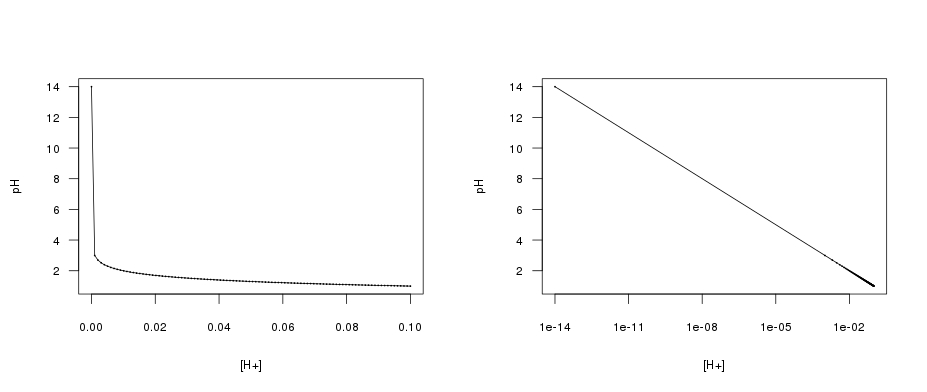
Questi due grafici rappresentano il pH in funzione della [H+].
Nota che i grafici rappresentano esattamente la stessa identica cosa, e i punti sono esattamente alle stesse coordinate.
Semplicemente passando da un sistema di coordinate cartesiano ad uno non-lineare quello che in un caso era una curva esponenziale diventa una linea retta.
Nota che non c'è stata alcuna trasformazione numerica dei punti, i valori sono sempre gli stessi nei due grafici, la trasformazione è puramente visuale. |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
Geeko
Utente
 

Città: Milano

1043 Messaggi |
 Inserito il - 05 novembre 2011 : 15:11:50 Inserito il - 05 novembre 2011 : 15:11:50




|
Perfetto, questo mi era chiaro. La mia citazione si riferiva proprio a questo "problema grafico" e non numerico. E tutto quello che hai scritto è molto chiaro. L'unica cosa che il mio cervello riesce poco a "visualizzare", per così dire, è il cambiamento della concavità tra le due curve nelle fasi iniziali (a basse concentrazioni). Cioè in (1) ho una concavità negativa (rivolta verso il basso), mentre in (2) la concavità è positiva relativamente agli stessi valori di [D].
Per quanto detto fin ora però credo che anche questo dipenda da quella specie di "stiramento" dell'asse delle ascisse nelle prime fasi e poi dalla sua progressiva "compressione" man mano che ci spostiamo a sinistra, verso valori esponenzialmente più grandi...sempre perché ci troviamo in un piano semilogaritmico...o almeno direi questo se dovessi rispondere a naso... 
ps. perché la prima curva non è proprio un'iperbole? Sarà una porzione di un ramo di iperbole allora..no? |

|
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 05 novembre 2011 : 16:30:34 Inserito il - 05 novembre 2011 : 16:30:34




|
Citazione:
Cioè in (1) ho una concavità negativa (rivolta verso il basso), mentre in (2) la concavità è positiva relativamente agli stessi valori di [D].
Per quanto detto fin ora però credo che anche questo dipenda da quella specie di "stiramento" dell'asse delle ascisse nelle prime fasi e poi dalla sua progressiva "compressione" man mano che ci spostiamo a sinistra, verso valori esponenzialmente più grandi...sempre perché ci troviamo in un piano semilogaritmico...o almeno direi questo se dovessi rispondere a naso..
Ho rifatto il tuo grafico mettendo delle linee verticali equidistanti (ancora una volta, nota che i due grafici sono identici, cambia solo la rappresentazione. Le linee sono distanti 5 sia a destra che a sinistra). Come puoi vedere nel grafico a destra le linee sono spaziate sempre meno. Aggiungi a questo il fatto che la curva all'inizio cresce molto velocemente e poi "rallenta", ed ecco la spiegazione (grafica) delle due concavità diverse (sono sicuro si possa fare una spiegazione matematica... ma al momento non ho veramente voglia di pensarci!).
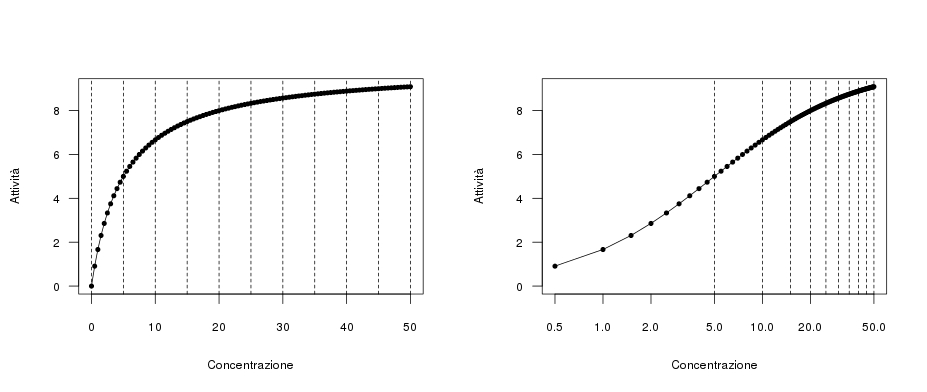
Citazione:
perché la prima curva non è proprio un'iperbole? Sarà una porzione di un ramo di iperbole allora..no?
Era solo per essere pignolo... un'iperbole avrebbe anche un asintoto verticale, e quella non ce l'ha, ma fa nulla
PS: per chi volesse giocarci un po' ecco il codice in R che ho usato per ottenere il grafico
mm <- function(conc, Vmax, Km)
{
return ((conc*Vmax)/(Km+conc))
}
conc <- seq(0, 50, 0.5)
Km <- 5
Vmax <- 10
par(mfrow=c(1,2))
plot(conc, mm(conc, Vmax, Km), type="o",
pch=20, las=1, cex=0.9,
xlab="Concentrazione", ylab="Attività")
abline(v=seq(0, 50, 5), lty=2)
plot(conc, mm(conc, Vmax, Km), type="o",
pch=20, las=1, cex=0.9, log="x",
xlab="Concentrazione", ylab="Attività")
abline(v=seq(0, 50, 5), lty=2)
|
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
Geeko
Utente
 

Città: Milano

1043 Messaggi |
 Inserito il - 05 novembre 2011 : 18:14:37 Inserito il - 05 novembre 2011 : 18:14:37




|
Grazie mille Chick!  I due grafici sono venuti molto bene, e penso di avere capito. E penso anche che l'asintoto verticale ce l'abbia, ma si trova sul semipiano negativo...e ai fini del modello è come se non lo avesse. I due grafici sono venuti molto bene, e penso di avere capito. E penso anche che l'asintoto verticale ce l'abbia, ma si trova sul semipiano negativo...e ai fini del modello è come se non lo avesse. |

|
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 05 novembre 2011 : 18:41:38 Inserito il - 05 novembre 2011 : 18:41:38




|
Citazione:
E penso anche che l'asintoto verticale ce l'abbia, ma si trova sul semipiano negativo...e ai fini del modello è come se non lo avesse.
Beh, ma visto che nè l'attività nè la [] possono essere negative...
Matematicamente, un'iperbole è genericamente definita come
Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0
Qui siamo nel caso di
y = ax/(b+x)
elevando al quadrato entrambi e semplificando un po' arrivi a
-ax^2 + x^2y^2 + 2bxy^2 + by^2 = 0
Come vedi hai dei termini in più (il termine in x^2y^2 e quello in xy^2) che non ci sono nell'equazione dell'iperbole :) |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
Geeko
Utente
 

Città: Milano

1043 Messaggi |
 Inserito il - 06 novembre 2011 : 15:31:03 Inserito il - 06 novembre 2011 : 15:31:03




|
L'equazione che descrive questi fenomeni era
(LR/Ro) = [D]/(Kd + [D])
dove
LR: numero di recettori o siti attivi occupati
Ro: numero di recettori o siti attivi totali
[D]: concentrazione di ligando o farmaco
Kd : costante di dissociazione del ligando con quel sito attivo
Quindi considero il rapporto (LR/Ro) come la variabile dipendente y, e [D] come x.
Nel nostro caso i due asintoti quindi corrispondono a:
x = -Kd (verticale)
y = 1 (orizzontale)
Perciò l'asintoto verticale sta a una distanza dall'origine pari a "Kd" sul semipiano negativo delle x, torna tutto?  |

|
 |
|
| |
Discussione |
|
|
|
Quanto è utile/interessante questa discussione:
| MolecularLab.it |
© 2003-18 MolecularLab.it |
 |
|
|














